MATEMÁTICA, FILOSOFÍA Y TRASCENDENCIA
Platón escribió sobre la puerta: «Que sólo entren los geómetras». Los tiempos han cambiado. La mayoría de aquellos que ahora buscan ingresar al mundo intelectual de Platón ni saben matemática ni experimentan contradicción en un desobediencia al mandato. La escisión patológica de nuestra cultura entre «humanidades» y «ciencia» apuntala su seguridad. Platón era un filósofo, y la filosofía pertenece a las humanidades con la misma certeza con que la matemática pertenece a las ciencias».
Seymour Papert, Desafío a la Mente. Cap. 2
Una de las característica que más he apreciado del movimiento Logo iniciado en los 80 en Argentina es que sus iniciadores tenían en común un enfoque quasi renacentista, donde se integraban las ciencias duras, entre ellas la computacional, con las humanidades. La filosofía, el arte, la educación como práctica y como ámbito de reflexión, eran una constante en su discurso de capacitación. Yo fui particularmente sensible a este enfoque. Ya cuando estaba en el profesorado de química me fascinaban las clases de Filosofía, al punto que el docente me incitaba a abandonar la química. Creo que era el único de los 25 que conformaban el curso que participaba de ese entusiasmo. Para el resto la filosofía no tenía nada que hacer en el ámbito de la ciencia.
LOGO, más allá de sus cualidades como lenguaje de programación, me impactó en esa época porque lo relacioné enseguida con el concepto del Logos enunciado por Heráclito en los albores de la Grecia clásica. Pero también tenía para mi hasta ecos religiosos. El Evangelio de Juan (año 100 DC), muy influenciado por la filosofía griega, fue escrito en griego. Su primer versículo dice: «En el principio era el Verbo, y el Verbo era con Dios, y el Verbo era Dios». La palabra original traducida por Verbo era justamente LOGOS. En el principio era el LOGOS. Los nombres son importantes por los significados que les damos. En comparación, SCRATCH ¿qué puede significarme?.
Pero no todo era filosofía y religión. Mientras la mayoría de mis compañeros veían una tortuga yo veía un vector. Cada imagen programada con dificultad era una suma vectorial. Cuando hice un círculo me di cuenta que la tortuga generaba la curva mediante una sucesión de «diferenciales». El rumbo (o sea la inclinación de la tangente) de cada diferencial variaba en forma lineal, porque que la derivada de una cuadrática es una función lineal.
Todo esto era muy poderoso. Además te daba poder para generar infinitas formas y entender conceptos complejos. La tortuga era un objeto matemático serio, un invento genial. En 30 años no he visto nada igual.
Y todo esto se comunicaba mediante el LOGOS, la palabra, el verbo, la acción, que la tortuga mediatizaba en la pantalla.
VECTORES Y DIFERENCIALES
PITÁGORAS: MATEMÁTICA Y MISTICISMO
Pitágoras nació en el 569 AC en la isla de Samos, en el paradisíaco mar Griego, casi pegado a Persia. No hay muchos datos sobre su vida. No dejó ningún escrito y todo lo que sabemos es por medio de sus discípulos que habitualmente le atribuyeron todos sus descubrimientos.
Por ellos sabemos que viajó por el mundo civilizado de entonces, especialmente Egipto y Babilonia, culturas que influyeron intensamente en sus conocimientos y vida. Los egipcios son considerados los «inventores» de la geometría, palabra que significa «medición de la tierra», y cuyos conocimientos aplicaban a marcar las tierras que anualmente eran barridas por el Nilo. Desarrollaron una aritmética empírica y utilitaria, aunque suelen encontrarse con papiros conteniendo problemas abstractos. Los egipcios conocían las relación de la tríada [3 4 5], una de las tríadas formada por números enteros que cumplen con la relación pitagórica. En Babilonia además de conocimientos astronómicos, Pitágoras recibió de los sacerdotes que ejercían la ciencia matemática, la convicción de una relación imprescindible entre matemática y religión.
De regreso a Samos se destacó como un hombre de extraordinario intelecto pero al mismo tiempo de ideas exóticas que evolucionarían hacia una nueva religión basada en la creencia de que la materia con que está hecho el Universo es el número. Su creencia estaba alimentada no solo por la religiosidad que había absorbido en los astrónomos y matemáticos babilónicos, sino por la matemática misma que permitía describir un orden en las relaciones de la belleza, de los intervalos musicales y del movimiento de los planetas. Si nos ponemos a pensar, es sorprendente que casi todo sea «numerable» o «calculable». Hasta el alma parece que pesa 21 gramos. Esa admiración se transformó en una nueva religión que sobrevivió varios siglos a su creador. Sus ágoras académicos se transformaron en una Gran Hermandad, sus alumnos pasarían a ser sus discípulos y él, su profeta.
A Pitágoras se le atribuye la invención del álgebra y del método deductivo que utiliza para realizar demostraciones imposibles desde el método empírico. Por ejemplo los egipcios sabían que la raíz de 2 no podía reducirse a un número fraccionario. Siempre que se divide se llega a un resto diferente de 0. Puedo hacer la división hasta 100000 veces pero, ¿cómo saber que en la 100001 se llegará al mismo resultado?. Pitágoras demostró la irreductibilidad de la raiz de 2 mediante el método de reducción al absurdo. Sus genialidades se ven opacadas por suspuestos religiosos que no tenían la rigurosidad de su pensamiento, por ejemplo los números tenían sexo, machos los impares, hembras los pares. Enseñaba que el primer número era el 3, pues el 1 era indivisible y el 2 hembra :=). El 5 se asociaba al matrimonio pues era la suma del primer número hembra con el primer número macho. «Pitágoras y su teorema en 90 minutos» de Paul Strathern, es un breve texto que describe amenamente el pensamiento y la religiosidad del gran matemático.
Escultura de Pitágoras en Samos.
EL TEOREMA DE PITÁGORAS
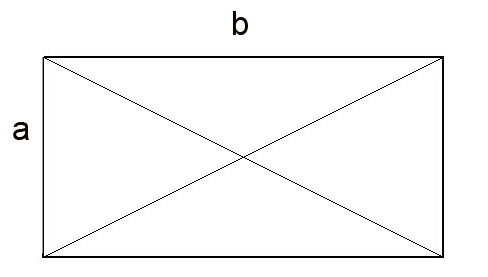
Me he sorprendido al leer el texto de Strathern que el teorema tiene más de 400 demostraciones diferentes. Los chinos dejaron una de ellas en un texto del Siglo V AC. En su forma simplificada puede verse abajo. Se trata de un cuadrado cuyo lado es la suma de las longitudes de 2 catetos a y b, siendo d la hipotenusa del triángulo rectángulo. A su vez d es el lado del cuadrado grisado. Según Strathern esta demostración encierra una gran belleza.
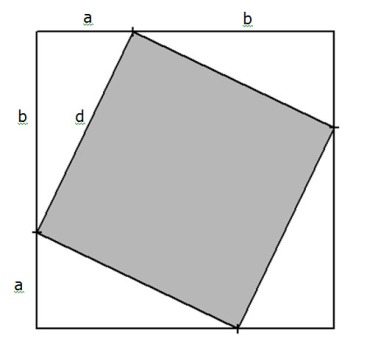Sup. Cuadrado externo = (a + b)2
Sup. triángulo = b*a/2
Sup. cuadrado gris = d2
d2 = (a + b)2 – 4. (a*b/2)
d2 = a2 + b2 + 2ab – 2ab
d2 = a2 + b2
Como d es la hipotenusa del triángulo y a y b sus catetos
H2 = a2 + b2
Con lo que queda demostrada la relación.
PROGRAMANDO LA CAJA CHINA
Programemos en FMS LOGO un procedimiento con 2 inputs que definen los 2 catetos :A y :B. No incluiremos el relleno del cuadrado interior.
PARA CAJA_CHINA :A :B
REPITE 4 [AV :A GD 90 AV 5 RE 10 AV 5 GI 90 AV :B GD 90]
AV :A
MAKE «HIPO POTENCIA :A*:A+:B*:B 1/2 (calcula la hipotenusa aplicando Pitágoras) (1)
MAKE «ANG ARCTAN :A/:B (calcula el ángulo que debe girar para trazar el segmento d)
GD :ANG
REPITE 4 [AV :HIPO GD 90]
FIN
(1) POTENCIA es un comando Logo con 2 inputs POTENCIA BASE EXPONENTE. El exponente 1/2 corresponde a una raíz cuadrada.
EL TEOREMA, 1/3 DE LA FELICIDAD
He enseñado a muchas generaciones que el conocimiento del Teorema de Pitágoras nos asegura 1/3 de la felicidad. Claro que se trata de una hipérbole (no hipérbola), que enfatiza el poder y la importancia del pensamiento matemático y particularmente algebraico.
Los otros 2/3 los dejo para otra oportunidad.
Sucede que me he encontrado con este teorema en innumerables problemas especialmente de física. Así en la suma vectorial el método cartesiana consiste en reducir cada vector a sus 2 componentes ortogonales Vx y Vy (en el plano) Las componentes ortogonales pueden sumarse aritméticamente pues están en la misma dirección y las resultantes ortogonales quedan conectadas con la resultante mediante Pitágoras.Es un caso especial de una heurísitica que reduce un problema complejo a problemas simples.
En cierta forma ésto es parte de la felicidad.
TRIÁNGULOS PITAGÓRICOS
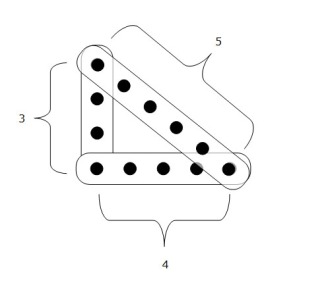
Se denominan así a aquellos cuyos catetos e hipotenusa tienen longitudes enteras. Ya hemos mencionado que los egipcios conocían la tríada [3 4 5], ya que 32 + 42 = 52
ESCUADRA MECCANO 3 4 5
Yo me encontré con esta tríada cuando intentaba realizar una escuadra con Meccano. Las piezas Meccano pueden medirse por sus agujeros que son proporcionales a la longitud de la pieza. Una tira de 6 agujeros tiene 5 espacios, las de 5 agujeros, 4 espacios y la de 4 agujeros, 3 espacios. Una escuadra se determina por piezas que tengan una relación de espacios enteras, ya que no se puede poner un tornillo a 4,5 espacios. Esta es una razón para tener un stock de tiras de 6 agujeros (5 espacios) pues se utilizaran con mayor frecuencia que otras.
¿Qué otras tríadas pitagóricas hay de números enteros?. Son infinitas.
Hagamos un procedimiento LOGO que por iteración busque esas tríadas para valores entre 1 y 100.
PARA ENTERO? :NU
DEV (ENTERO :NU) = :NU
FIN
PARA PITAENTEROS
MAKE «SOLUTIONS []
PITAENTERO2 1 1
ES CUENTA :SOLUTIONS
ES :SOLUTIONS
FIN
PARA PITAENTERO2 :C1 :C2
SI :C2 > 100 [alto]
PITAENTERO1 :C1 :C2
PITAENTERO2 :C1 + 1 :C2 + 1
fin
PARA PITAENTERO1 :C1 :C2
SI :C1 = 100 [alto]
MAKE «HIP POTENCIA (:C1*:C1 + :C2*:C2) 1/2
SI ENTERO? :HIP [MAKE «SOLUTIONS PONPRIMERO (LISTA :C1 :C2 :hip) :SOLUTIONS]
PITAENTERO1 :C1 + 1 :C2
fin
Resultado:
63 tríadas
[84 80 116] [100 75 125] [96 72 120] [92 69 115] [88 66 110] [72 65 97] [84 63 105] [91 60 109] [80 60 100] [63 60 87] [76 57 95] [90 56 106] [72 54 90] [68 51 85] [90 48 102] [64 48 80] [55 48 73] [60 45 75] [56 42 70] [96 40 104] [75 40 85] [42 40 58] [80 39 89] [52 39 65] [77 36 85] [48 36 60] [84 35 91] [56 33 65] [44 33 55] [60 32 68] [72 30 78] [40 30 50] [96 28 100] [45 28 53] [36 27 45] [60 25 65] [70 24 74] [45 24 51] [32 24 40] [72 21 75] [28 21 35] [99 20 101] [48 20 52] [21 20 29] [80 18 82] [24 18 30] [63 16 65] [30 16 34] [36 15 39] [20 15 25] [48 14 50] [84 13 85] [35 12 37] [16 12 20] [60 11 61] [24 10 26] [40 9 41] [12 9 15] [15 8 17] [24 7 25] [8 6 10] [12 5 13] [4 3 5]
PERÍMETRO Y SUPERFICIE
Entre las tríadas pitagóricas hay 2 que cumplen con una singular condición, la superficie es igual al perímetro. Hagamos los procedimientos para que Logo busque iterativamente estas 2 tríadas, teniendo en cuenta que la tríada [A B C] es la misma que [B A C].
PARA TRIANPITA
BT MAKE «SOLUTIONS []
TRIANPITA2 1 1
ES :SOLUTIONS
SUPPERI :SOLUTIONS
FIN
PARA TRIANPITA2 :c1 :c2
ES :c2
SI :c2 > 100 [ALTO]
TRIANPITA1 :c1 :c2
TRIANPITA2 :c1 + 1 :c2 + 1
fin
PARA TRIANPITA1 :c1 :c2
ES fRASE :C1 :C2
SI :c1 = 100 [alto]
MAKE «hip potencia (:c1*:C1 + :c2*:C2) 1/2
MAKE «peripita :c1 + :c2 + :hip
MAKE «suppita :c1 * :c2 / 2
SI :peripita = :suppita [MAKE «SOLUTIONS PONPRIMERO (LISTA :c1 :c2 :hip) :SOLUTIONS ]
TRIANPITA1 :c1 + 1 :c2
fin
PARA SUPPERI :L
SI VACIO? :L [ALTO]
TYPE PRIMERO :L TYPE CAR 32
(TYPE [PERIMETRO=] (ITEM 1 PRIMERO :L) + (ITEM 2 PRIMERO :L) + (ITEM 3 PRIMERO :L))
TYPE CAR 32
(ES [SUPERFICIE =] (ITEM 1 PRIMERO :L) * (ITEM 2 PRIMERO :L) / 2)
ES []
SUPPERI MP :L
FIN
Resultados:
[8 6 10] [12 5 13]
8 6 10 PERIMETRO=24 SUPERFICIE = 24
12 5 13 PERIMETRO=30 SUPERFICIE = 30
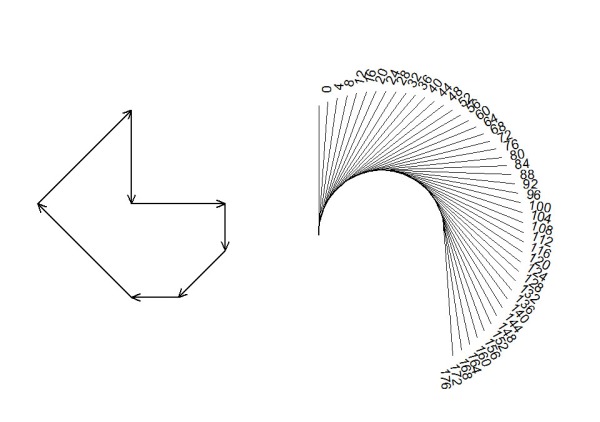
PITÁGORAS POR APROXIMACIÓN
Trazar las diagonales de un rectángulo conocidos el alto y el ancho es un problema que necesita trigonometría para calcular el ángulo de la diagonal.
En LOGO una solución es:
para recdiago :a :b
pongrosor 2
repite 2 [av :a gd 90 av :b gd 90]
make «angudiago arctan :b/:a (calcula el ángulo)
make «diago potencia (:a*:a + :b*:b) 1/2 (calcula la diagonal aplicando Pitágoras)
pongrosor 1
gd :angudiago
av :diago
re :diago
gi :angudiago
av :a
gd 180 – :angudiago
av :diago
FIN
RECDIAGO 200 400
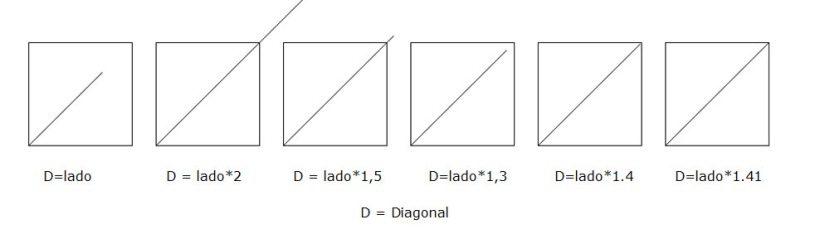
El ángulo de la diagonal (la hipotenusa) es una función del alto y el ancho. En el caso de un cuadrado el ángulo es 45° y la diagonal una función del lado. Es posible hacer una determinación empírica aproximada de la diagonal.
PARA CUA :LADO :CO
REPITE 4 [AV :LADO GD 90]
GD 45
AV :LADO * :CO
FIN
Probando con distintos factores (:co) podemos encontrar que la diagonal (o sea la hipotenusa de cualquiera de los 2 triángulos interiores) es aproximadamente 1.41 * :lado. Este valor es la RAIZ de 2 con sólo 2 decimales.
Esto está de acuerdo con el teorema de Pitágoras. En este achivo encontrarás una descripción: la-tortuga-robot-y-el-mundo-geometrico
CUADENTROS. DESAFÍOS Y CREATIVIDAD PITAGÓRICA
Estos son 2 diseños de CUADENTROS creados por alumnos de 1° año. Los CUADENTROS son figuras geométricas diseñadas dentros de un cuadrado y generadas por segmentos ortogonales y diagonales que están en una relación sencilla del lado del cuadrado. 1/2 1/3 1/4 1/6. La relación de la diagonal 1.41 se determina por aproximación.
 ROCKET – LUZ |
 EMBUDO – EMILIANO |
| PARA ROCKET_LUZ :LADO BL REPITE 4 [AV :LADO GD 90] GD 90 AV :LADO/3 GI 90 AV :LADO/3 GI 90 AV :LADO/6 GI 45 AV :LADO *1.414/6 GD 45 GD 90 AV :LADO/2 GD 135 AV :LADO * 1.414/6 GI 45 AV :LADO/6 GI 90 AV :LADO/2 GD 135 AV :LADO * 1.414/6 GI 90 AV :LADO * 1.414/6 GD 135 AV :LADO/2 GI 90 AV :LADO/6 GI 45 AV :LADO * 1.414/6 GD 135 AV :LADO/2 GD 135 AV :LADO * 1.414/6 GI 45 AV :LADO/6 GI 90 AV :LADO/3 GD 135 AV :LADO * 1.414 / 6 GI 90 AV :LADO * 1.414/6 SL GD 45 AV :LADO/3 GD 90 AV :LADO/3 GD 90 AV :LADO/6 AV :LADO/3 RELLENA GD 90 AV :LADO/3 GD 90 AV :LADO/2 GD 90 FIN |
PARA EMBUDO :LA BL repite 4 [av :la gd 90] av :la/6 gd 90 av :la/2 gi 90 av :la *2/6 gi 45 av :la *1.414/2 gd 135 av :la gd 90 av :la * 1/4 gd 90 av :la /4 gd 135 av :la *1.414 /4 gd 135 av :la gd 90 av :la/2 gd 90 sl av :la *3/4 rellena re :la *3/4 gi 90 av :la/2 gd 90 fin
|
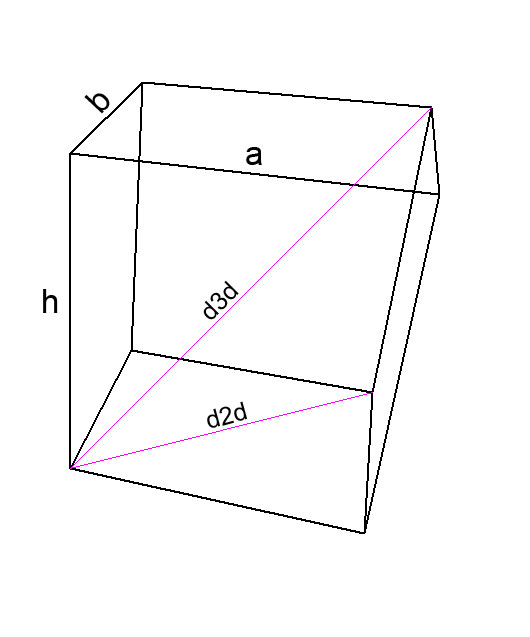
PITÁGORAS 3D
Finalmente apliquemos LOGO para graficar las diagonales de un paralelepípedo.
para parale :a :b :h
pongrosor 2
poncl 0
repite 2 [repite 2 [av :h gd 90 av :a gd 90]
gd 90
av :a gi 90
rightroll 90
repite 2 [av :h gd 90 av :b gd 90]
gd 90
av :b gi 90 rightroll 90]
make «d2d potencia :a*:a + :b*:b 1/2 (calcula la diagonal de la base)
make «angudia2d arctan :b/:a
make «d3d potencia :d2d*:d2d + :h*:h 1/2 (calcula la diagonal espacial del paralelepípedo)
make «angudia3d arctan :h/:d2d
rightroll :angudia2d
gd 90
pongrosor 1 poncl 5
av :d2d
re :d2d
gi :angudia3d
av :d3d
fin
PITÁGORAS Y LA EDUCACIÓN
En la época que vivimos la Educación se ha convertido en una subsidiaria de las TIC. El mercado domina el pensamiento y con sus cantos de sirena empujan una dependencia no solo tecnológica, sino principalmente sicológica. Los fundadores del Logo tenían otra cosmovisión de la tecnología y la educación. Solo era válida la tecnología que nos demandaba esfuerzo y creación, en lugar de la actual valoración de la sustitución y la velocidad. El conocimiento y en particular el matemático está cuestionado y parece prevalecer una concepción utilitaria. Para Pitágoras la matemática regía el mundo, pero no como ciencia de lo útil, sino como organizadora de la mente,como formadora del pensamiento. En su afan místico los pitagóricos crearon normas y preceptos que hoy nos darían risa, pese a todo, no solo el teorema de Pitágoras mantiene actualidad. El genio de Samos nos dejó también pensamientos que iluminan.
EN EL PRINCIPIO ERA EL LOGO 